The hill-climbing search algorithm (steepest-ascent version) […] is simply a loop that continually moves in the direction of increasing value—that is, uphill. It terminates when it reaches a “peak” where no neighbor has a higher value. The algorithm does not maintain a search tree, so the data structure for the current node need only record the state and the value of the objective function. Hill climbing does not look ahead beyond the immediate neighbors of the current state. This resembles trying to find the top of Mount Everest in a thick fog while suffering from amnesia.

(Russell & Norvig, 2010: 122)

The wind was icy, and the weather, no, one couldn’t call it good! Thick clouds that were growing ever more gray and blue-black hung down deeply; the cold slopes all around, whose details began to be more sharply visible, massive and brazen nearby, on both sides losing themselves up in the marvelousness of ravines and distance, disappeared up into dark, smoky, severe gray fog; there was no clear view of anything at a great height: and yet everything was waiting up there, cliffs and glaciers and crashes, dark chimneys, frightful storms, unspeakable exertions…

(Hohl, 2012 [1975]: 30)

The Ascent of Knowledge

Where is the privileged site of knowledge today? ‘Prophecies are no longer proclaimed from the mountaintop but from the metrics’, write Arjun Appadurai and Paula Kift (2020), warning of the emplacement of quantification at the very apex of knowledge production. Neither Sinai, nor Sri Pada, nor Olympus, nor Fuji, but Number, set on high with solid footing and a place of normative exception from which to speak.

Our metric societies are obsessed with the precise measurement of deviation and error; everything is to be optimized, but to questionable ends. Meanwhile, the essential computability of reality is taken for granted, or else the question is sidestepped entirely: what matters most is that an algorithm works (or is thought to work), less often how or why. Despite this, the new machine learning systems will, we are told, eventually realize human-level artificial general intelligence (AGI): the holy grail of the quantified society. Surveyed from the lofty heights of algorithmic rationality, entire worlds unfold as vast terrains of data—measurable and mappable—receding towards the horizon.

While the drive towards ever more precise metrics and more powerful machine learning systems may have displaced physical mountaintops and introspection, dialogue, or divine revelation as favored grounds upon which to erect truth claims, the potency of the mountain as cultural symbol and ideological backdrop has hardly dissipated. Judging by the language that machine learning practitioners use to describe how today’s most advanced neural networks are themselves produced, or ‘trained,’ the mountain landscape remains as compelling and potent an emblem as ever. Transformed into an image and metaphorical framework used to intuit and understand what happens within an opaque algorithmic learning process, the mountain persists as a ghostly terrain upon which machines are imagined to learn.

This paper takes as its object of analysis a recurring allegory about a lone hero’s journey across a mountainous landscape—an allegory which appears again and again in machine learning discourses as an explanatory trope and conceptual tool. Allegorical passages like the one which opens this paper, from Stuart Russell and Peter Norvig’s standard introductory textbook Artificial Intelligence: A Modern Approach, are often deployed by practitioners to describe the functioning of a particularly important yet difficult to predict algorithmic approach: gradient optimization, or simply the gradient method.

The gradient method, alongside the availability of massive data sets and increased computing power, has been critical to recent breakthroughs made in machine learning research: the method and its secondary derivations are the de facto means by which the vast majority of today’s machine learning systems are trained (Ruder, 2017: 1). ‘If you had to throw out your entire machine-learning toolkit in an emergency save for one tool’, Pedro Domingos extols, gradient optimization ‘is probably the one you’d want to hold on to’ (2015: 109). ‘Over the last decade, a single algorithm has changed many facets of our lives’, opens a recent gradient optimization paper, referring to one of the most popular implementations (Parker-Holder et al., 2020: 1). If the recent explosion of research and hype about machine learning, and Deep Neural Networks (DNN’s) in particular, has led to these terms being used metonymically to stand in for the entire field of AI research as a whole, then it is no stretch to consider gradient optimization to be the algorithmic kernel at the heart of much of this hype. Without the gradient method and its allied techniques, there would be no ‘AI revolution’ in sight.

This paper is less about the technical efficacy of the method itself, however, and more about how the method is communicated and mediated through allegorical language and visualizations which install the mountain landscape once again as the privileged site of learning, knowledge, and improvement. The allegorical stories which are used to explain the method, and which are the main focus of this paper, exhibit a remarkable consistency: gradient narratives, as I term them, re-present complex algorithmic processes in explicitly spatial, embodied, and narrative terms. Most of today’s computer science students come to understand how gradient optimization works through just such metaphorical constructions; these quasi-heroic tales thus play an important educational and heuristic role in the continuity of machine learning as a sociotechnical practice and economic force. As a coherent body of discourse and set of visual conventions, gradient narratives and the images they accompany constitute integral elements in the infrastructural and mythic scaffolding that underlies contemporary data capitalism. Divine knowledge has its summits; gradient knowledge has them too.

In the machine learning field, gradient narratives are understood to be useful because the processes they describe are often difficult to interpret. As Sebastian Ruder puts it, ‘[g]radient descent optimization algorithms, while increasingly popular, are often used as black-box optimizers, as practical explanations of their strengths and weaknesses are hard to come by’ (2017: 1). As this problem of interpretation and constitutive doubt has become more widely recognized, it has led to charges of ‘alchemy’ from insiders and outsiders alike (Hutson 2018).¹ Insofar as gradient narratives present the process of machine learning as a story or image about a protagonist navigating a landscape, they offer practitioners a ready means for grasping these processes in intuitive, anthropomorphized, and culturally familiar terms. Visualized, the results can be immensely compelling, conveying an immediate sense of ‘how we got here’—with ‘here’ signifying not an actual location in physical space, but the outcome of a training process, the behavior of an algorithm, and a particular, optimized configuration of the system’s internal variables and architecture.

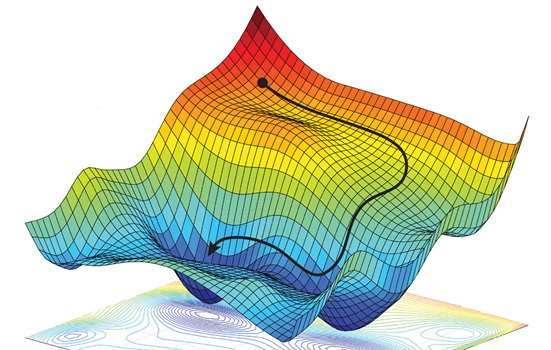
The basic contours of gradient narratives are familiar: learning is a journey; one’s objective is a destination. The protagonists, which stand in for machine learning models undergoing optimization, have clear objectives: to reach either the highest or the lowest point on the surrounding landscape (gradient ascent or descent, respectively). Such points signify an ideally optimized machine state; the purpose of gradient optimization is to iteratively find one’s way to such a desired high or low point by traversing the landscape, step by step. The protagonists in these narratives, however, are typically faced with improbable odds of success, reflecting the constiuitive uncertainty of the very processes they describe. It might be easy to get sidetracked by a false summit, stuck on a ridge, or disoriented on a wide plateau. Due to this constitutive uncertainty, the question of how an algorithmic protagonist should reach its objective (thus attaining a state of maximal optimization) is a question of intense ongoing study in the field, frequently posed in the same metaphorical language of landscape and navigation. In practice, however, the problem is usually addressed through a combination of precedent, trial and error, superstition, and chance.

The experientially grounded narratives and visualizations this paper analyzes provide practitioners interpretive frames through which to understand these conditions of uncertainty and grapple with the abstract mathematical relationships in play. Through them, practitioners come to terms with what it means to ‘fit’ a model to reality and what it means, ultimately, to optimize and to ‘learn’. Thrown into the proverbial shoes of the personified algorithm as it traverses a multi-dimensional error or loss surface replete with peaks, valleys, plateaus, saddle points, ridges, canyons, and cols, practitioners are better able to identify with the workings of an often unpredictable and opaque nonhuman process, coming to grips with its triumphs and failures in heroic terms.² But lost on foot, few question the larger structure and epistemic status of the imagined world that lies before them, nor ask what kinds of assumptions or oversights such narratives might carry with them or obscure.

Much ink has been spilled addressing the constitutive role of language, particularly metaphor, in the social production of science; likewise, visualization has long played an important role in the conception and communication of abstract theories, scientific or otherwise. ‘The intuitive appeal of a scientific theory’, write George Lakoff and Mark Johnson, ‘has to do with how well its metaphors fit one’s experience’ (1980: 19). For Donna Haraway, in her early work on the shaping of embryos, ‘[m]etaphor is a property of language that gives boundaries to worlds and helps scientists using real languages push against those bounds’ (2004: 10). And for Philip Agre, reflecting on AI in particular, ‘[e]ach technique is both a method for designing artifacts and a thematics for narrating its operation’ (1997: 141). Narratives thus give form to the technoscientific worlds we inhabit, just as they give working practitioners concepts to experiment with, build upon, and tear down.

Here, I offer a genealogy and analysis of contemporary gradient narratives, both as constitutive elements in the production of machine learning models and as ideological reflections of the social milieus in which they circulate. The essay unfolds in two stages. First, I introduce the gradient method and sketch the history of its crystallization as an optimization technique by following three intertwined influences—what I refer to here as pathways. I describe the algorithm itself, dwell on the emergence of early scientific and mathematical models taking their inspiration from mountain landscapes, and touch on the importance of digital computation to the broad adoption of optimization methods. In this genealogy, I focus on a series of frequently cited paradigmatic models and examples which have been influential to later research and give texture to today’s machine learning field. My intent in choosing these examples is not to establish an authoritative history or to install a teleology, as though the pathways followed were somehow natural or inevitable; taking a cue from mountain landscapes themselves, I instead propose thinking about each example as something like a cairn or waypoint marking one of many possible trajectories across open terrain. Analyzing a series of historical reference points and their links in this manner, this essay contributes to a growing understanding of machine learning’s prehistory by tracing the roots of some of its contemporary stylistic, narrative, and visual conventions.³

After mapping some of the historical trajectories that inform machine learning’s contemporary mythology, I then ask how and why the mountain mise-en-scène, as a particular kind of landscape rich in cultural connotations and ideological associations, has persisted with such potency at the heart of data-driven knowledge production. While many alternative metaphors have been used over the years to describe gradient optimization, none has yet saturated the discourse so thoroughly or seriously challenged the mountain’s dominance as explanatory trope.⁴ As W. J. T. Mitchell has argued, a landscape is a medium, a ‘social hieroglyph’ and an expression of value, which functions by ‘naturalizing its conventions and conventionalizing its nature’ (1994: 5). What, then, are we to make of today’s technical machine learning literature, haunted as it is by metaphorical peaks and valleys shrouded in fog? Why are today’s deep learning algorithms always said to be climbing towards summits or descending ridges in search of low points? What, in other words, is being conventionalized or naturalized, beyond a superficial aesthetics, when we continually find the mountain at work in the machine?

The answer to these questions, I argue, is bound up not merely with the rehearsal of familiar religious or romantic imagery, the recapitulation of a Platonic metaphysics of ascension towards truth, or the crude projection of that which is materially disappearing into the sphere of the symbolic (although it is true that there are precious few unclimbed peaks remaining and entire mountain ranges are being strip-mined into oblivion). There is also, I argue, something like an ethos or orientation which is common to both cultures of machine learning and the mythos of modern mountaineering. Beyond numerous obvious differences, it is an orientational congruence, a shared dream, that accounts for the smooth transposition of stories about scaling peaks and navigating treacherous terrain onto technical explanations of machine learning and AI. I return to these questions in the latter part of this paper.

A Romance of Many Dimensions⁵

A comprehensive history of optimization would fill volumes. In what follows, I emphasize the confluence of three constitutive pathways that collectively ground gradient optimization as it is practiced today: the refinement of a mathematical algorithm, the articulation of a set of discourses and visual conventions about landscapes, and the development of a technology for performing calculations. The first pathway, on the concept of a gradient and the gradient algorithm itself, introduces the purpose and function of the method and briefly surveys the history of its invention and crystallization as a standard optimization procedure in mathematics. The second pathway, on landscape and navigation, traces how metaphors and visualizations of landscape were deployed and conventionalized across various scientific disciplines in the late 18^th and early 19^th centuries, such that their eventual uptake in optimization contexts appeared not only useful but natural. The third pathway, on computation and uncertainty, traces how the adoption of digital computers drastically enlarged the scope of applications which could be tackled with the gradient method, while also exacerbating the epistemological problems which still haunt its use. Afterwards, once all three pathways have been traced, I return to the question of the mountain mise-en-scène and its contemporary cultural and ideological dimensions.

I. Gradient

The first pathway I trace concerns the gradient method as a concept and as an algorithm. Both a straightforward mathematical procedure and a complex and unstable cultural object, the gradient method has proven eminently translatable between contexts. Distilled, it is an incredibly simple mathematical operation, powerful because of its simplicity when coupled with a machinic capacity for repetition. Its logic hinges on the more fundamental concept from which it derives its name: the gradient.

A gradient is any gradual transition or difference along a continuum. When mathematicians speak of gradients in a geometrical context today, they are usually speaking of a measure of a slope or angle: a derivative or a rate of change. Movement along any wave, curve, or smooth topological surface can be construed in terms of gradients, and these continuous forms are the grounds upon which the gradient method operates. While often implemented using digital computers today, the gradient method itself must be understood in distinction to methods that deal primarily with discrete or discontinuous phenomena, those in which the transition between two points happens across an irreconcilable break or gap (think, for example, of the difference between a sine wave and a square wave; the latter would repel the gradient method). This means that where the gradient method is used, the data and underlying relations are assumed to be essentially continuous, or else may be treated as such.

Beyond mathematics, however, the etymology of the term reveals an ambivalent double meaning. Gradient derives from the Latin gradus, meaning degree, but also step or stride (OED, 2020). The English term grade retains something of this ambivalence, referring both to an angle of incline, as in a road grade, and to a discrete stage or position in a hierarchy or procedure, as in levels of education. This double meaning persists, too, in how the gradient method functions: it is a method used to make iterative, discrete changes to a model, shifting that model’s output along a continuous line or surface step by step.⁶

The basic premise of the gradient method as it pertains to the optimization of mathematical models goes something like this. Say I have a function with a number of variables, mapping a set of inputs to a set of outputs, that I want to behave in a particular way. If I can compare the model’s actual output against the desired output, I can then calculate the model’s loss or error rate: a measure of the difference between what I want the model to return and what it actually returns. The idea behind optimization, today a mathematical field all its own, is to find reliable methods for progressively lowering a function’s error rate, or making the model ‘fit’ the desired output or data set as closely as possible. This is easier said than done: if the data are noisy and the model itself complex, it can be difficult to know which variables to change, and by how much. I could proceed by pure trial and error, plugging in variables at random, and this might work if I have only a few parameters and inputs. But imagine a situation with thousands of such variables, or millions, and mere trial and error quickly becomes untenable.

In these situations, having a systematic means of iteratively and gradually changing the variables in a function becomes a tremendous boon, and this is what optimization algorithms do. As such, most are relatively uncomplicated, one simply needs to run through them many times. Ideally, incrementally changing a function’s starting variables step by step would lead to the function eventually yielding the desired result—a state called convergence, wherein the desired and actual outputs coincide. If this can reliably be accomplished by an algorithmic system, then it matters less what the starting state of the model is or what the starting variables should be, any numbers will do, and the training algorithm will take care of the rest. This is more or less how training a machine learning model works today, effectively equating the term learning with that of optimization: error reduction as pedagogical paradigm.

In the geometrical interpretation of optimization, it is common to graph the error rate as a curved line or as a n-dimensional surface, with each dimension corresponding to a variable in the function. A model with thousands of variables would thus have thousands of dimensions, but for the purposes of visualizing and intuitively grasping the process, these many dimensions are often reduced and visualized in terms of only two or three. While numerous variations and implementations of the basic gradient method exist, each with particular characteristics and use cases, the underlying approach remains fundamentally the same: ‘climb’ to the highest state of optimization (gradient ascent or ‘hill-climbing search’) or ‘descend’ to the state of lowest error (gradient descent), in either case following the steepest angle of the line or surface. The ‘highest’ point would signify a state of ideal optimization or maximal accuracy; inverted, the ‘lowest’ point would correspond to the model which produces the lowest rate of error. In this context, the difference between ‘climbing’ and ‘descending’ is merely a matter of multiplying by -1; today it is a question of convention or preference which vertical orientation practitioners choose, although as the genealogy I undertake below makes clear, most historical examples have tended to favor ascent.

The history of the gradient method itself, before digital computation, is winding and uneven, proceeding in fits and starts. As is often the case in the history of mathematics, several people seem to have developed some version of the gradient method independently, apparently unaware of similar work undertaken elsewhere by others. Despite already existing for almost a century, it was only in the 1940s that anything close to a definitive story was proposed, when the method’s spread spurred newfound interest in its origins. Various other lineages have since been proposed, seeing continual revision as new overlooked figures are recognized and written into history (Petrova & Solov’ev, 1997).

Today, the method’s first formalization is usually credited to Augustin-Louis Cauchy in an obscure passage of his 1847 published works. There, it is proposed as a means of approximating the orbits of stars. Though Cauchy wrote that he would elaborate upon the method at a later date, he never did, and so his early contribution was, until the 1940s, frequently overlooked (Cauchy, 1847; Lemarechal, 2012; Petrova & Solov’ev, 1997). Indeed, for the first century after its formalization, Cauchy’s method was marginal in every sense: infrequently applied, little recognized, ‘rediscovered’ from time to time only to be forgotten once again and fade into obscurity.⁷

This changed during the Second World War and the years following, when the technique—soon being referred to as ‘hill-climbing’ or the ‘method of steepest-ascent’—was suddenly being deployed across a staggering range of fields. In 1944, while working for the U.S. Army at the Frankford Arsenal’s Fire Control Design Division, logician Haskell Curry noted that while the method remained largely unknown to authorities in numerical computation, it was already ‘standard procedure’ in a number of other, mostly applied, contexts (1944: 258).⁸ The purpose of Curry’s oft-cited paper was corrective and synthetic: to provide a summary and proof of the technique (something Cauchy had not provided), emphasizing its practical and applied relevance while noting that ‘[t]his method is not new’ (1944: 258).⁹

Curry’s emphasis on the method’s practical utility is unsurprising given his wartime research on fire control. While he did not provide visualizations, Curry’s paper had already begun using the topographical and embodied language of valleys, peaks, and steps that has since become second nature: ‘There is evidence that in practical problems these curves follow the natural valleys of the surface, so that each step brings us further toward the goal’ (Curry, 1944: 261).¹⁰ The immediate goal in this case was shooting down enemy aircraft, but Curry understood that the underlying method could, in principle, be applied to any problem that could be posed in terms of optimization along a continuum. After all, destroying a Japanese Zero was just a matter of fitting model to data: iteratively converging system and world.

Thus the gradient method—like the broader field of machine learning, and opposed to so-called symbolic AI—must not be considered deductive, properly speaking. Instead, it is probing and exploratory, with all of the doubled meanings and gendered undertones that these terms imply. The aim of contemporary machine learning research, as Luciana Parisi has noted, ‘is not to deduce the output from a given algorithm, but rather to find the algorithm that produces’ the desired output (2019: 92). This is precisely what the gradient method provides: a systematic, ‘step-wise’ means to search for an ideal model through incremental changes to a function’s constitutive parameters and variables, following the steepest rate of change up or down a loss surface.

As should already be clear by Curry’s language, posing the iterative, non-deductive problem of optimization in spatial and navigational terms provides a powerful and immediately graspable means for imagining how an algorithm might function or fail. As this exhaustive, iterative approach to modeling became more widely viable with digital computing, however, so would the problem of uncertainty. Further imagining and visualizing the method itself as a heroic protagonist, with the action unfolding on a specific kind of terrain—a vivid mountain landscape—arose to fill the interpretive void.¹¹

II. Landscape

‘The history of thought’, Fredric Jameson once wrote, ‘is the history of its models’ (1972: v). The second pathway I follow highlights some exemplary models incorporating navigational and landscape-based metaphors and visualizations from a number of scientific fields predating contemporary AI. Each of these models informed breakthroughs and new conceptualizations in their respective domains of knowledge and helped establish the visual and narrative conventions so commonplace in machine learning today. Such conventions, after all, did not appear out of nowhere; long before they were being used to interpret machine learning algorithms, landscape forms were adopted to visualize and render intuitive the workings of thermodynamics, the mysterious processes of biological evolution, and even the industrial production of chemicals on a mass scale.

A striking early example of a landscape model in action is that of the thermodynamic surface. First described by Josiah Willard Gibbs, the surface was then visualized by James Clerk Maxwell both as a map-like terrain on paper and as a tactile three-dimensional sculpted form.¹²

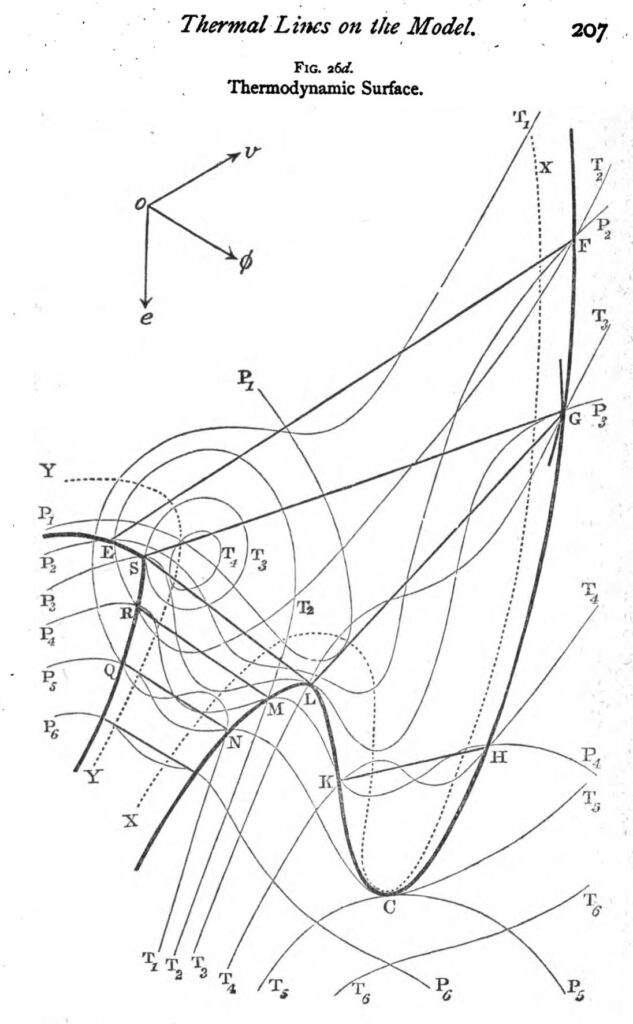
Gibbs was likely the first to conceptualize the complex behavior of thermodynamics in terms of an imagined surface, but he never went so far as to portray it visually, plotting it as though it really were a terrain. Maxwell, taking to Gibbs’ theory in the 1870s, reportedly spent an entire winter drafting and then sculpting a representation of Gibbs’ surface in clay before making several plaster copies and sending them off to colleagues (West, 1999; National Museum of Scotland, 2020). Different points on the thermodynamic surface correspond to different configurations of an imaginary substance’s energy, entropy, and volume, in turn mapped on to the sculpture’s three dimensions. These variables, of course, do not have an inherently geometric relationship of the kind that such visualizations portray, yet for Maxwell, rendering the relations between energy, entropy, and volume as a tactile surface also meant making these relations more immediately graspable and intuitive (West, 1999; Dragicevic, Jansen, & Vande Moere, 2020).

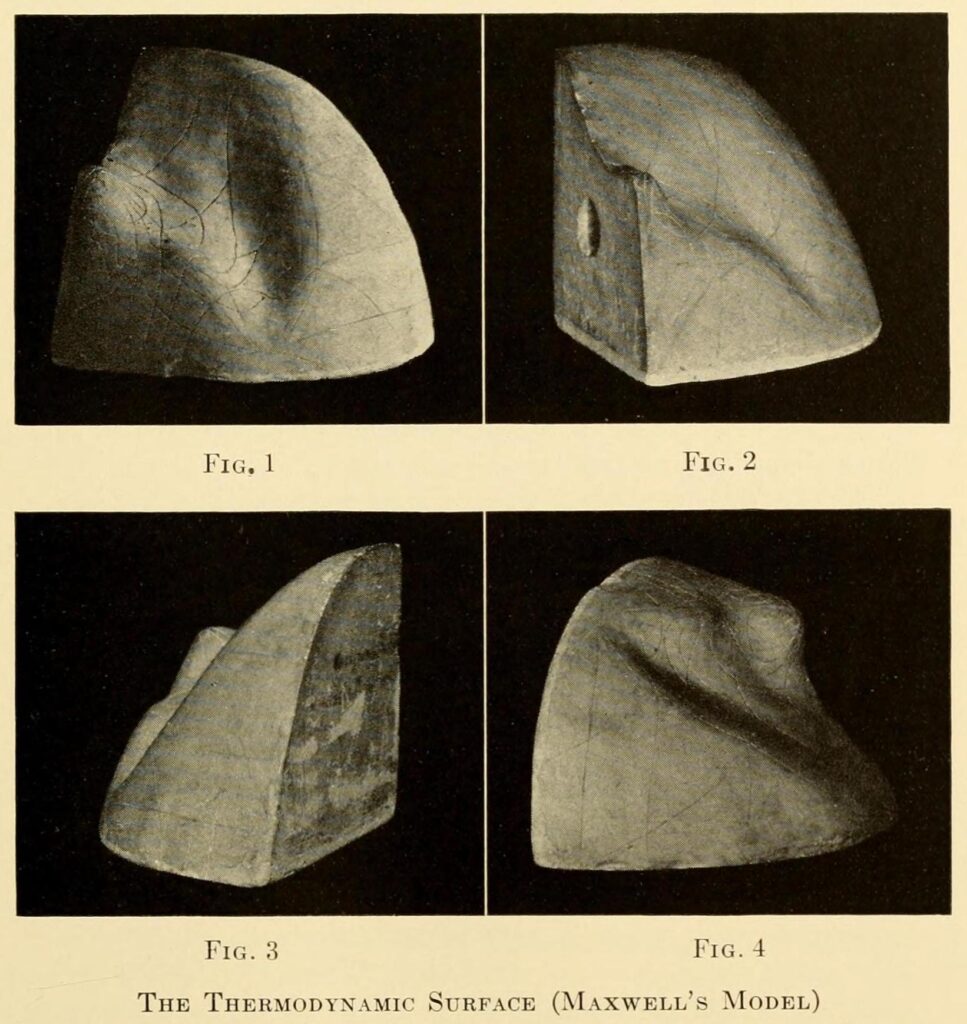
Recognizable in Gibbs and Maxwell’s surface is something like a landscape sensibility. Beautiful in the eyes of its creators, yet technical and exact in the spirit of what Gaston Bachelard disparagingly called ‘geometric intuition’ (Bachelard, 1964: 215), the thermodynamic surface serves as a rich example of an abstract mathematical relation represented in terms of landscape. Missing on this landscape, however, is an agent that would traverse it, much less a purposive protagonist finding its way; the idea was not optimization but understanding as such. And while the polished smudges on Maxwell’s sculpture betray a history of being touched and caressed (this is a sensuous as well as analytic object), this desire to trace form with finger, to explore a surface with one’s body and eyes, had not yet been incorporated into the symbolic logic of the model itself.

With a host of landscape-inspired scientific models that emerged in the 1930s and 1940s, however, protagonists would be placed definitively upon the surfaces they encountered. Exemplary is the adaptive landscape conceived by biologist Sewall Wright (1932), across which organisms and species were distributed: those higher on a hill were more ‘fit,’ and each species could be thought of as striving upwards to reach higher adaptive ground. According to Wright’s theory, a ‘species whose individuals are clustered about some combination other than the highest [point on the adaptive landscape] would move up the steepest gradient toward the peak, having reached which it would remain unchanged except for the rare occurrence of new favorable mutations’ (Wright, 1932: 357-358). The method of steepest ascent here is deployed as an analogy to make sense of the mysterious process of evolution. Wright continues:

In a rugged field […] selection will easily carry the species to the nearest peak, but there may be innumerable other peaks which are higher but which are separated by “valleys.” The problem of evolution as I see it is that of a mechanism by which the species may continually find its way from lower to higher peaks in such a field […] there must be some trial and error mechanism on a grand scale by which the species may explore the region surrounding the small portion of the field which it occupies.

(Wright, 1932: 358-359)

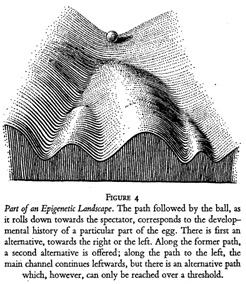
Consider, too, the epigenetic landscape proposed by Conrad H. Waddington (1940), which sought to metaphorically represent the way that genes guide the development of an individual organism as akin to how a stream or marble, navigating a series of furrowed slopes, would always be pulled downwards by gravity but could be influenced and rerouted by other factors. As both Jan Baedke (2013) and Susan Merrill Squier (2017) have shown, Waddington’s rich representational landscapes of complex (and hypothetical) epigenetic processes acted as heuristics and as persuasive communication and educational devices, helping to ensure the theory’s reception and longevity.

In both Wright’s and Waddington’s models, landscapes stood in for theoretical apparatuses of incredible complexity and uncertainty. Evolution and epigenesis were posed in the intuitive visual language of topography and gravity, climbing and descending. In each case, the landscape was something to be explored and interacted with, not just on a conceptual level as a heuristic, but within the world of the model itself. Mapping the progress of an agent across a landscape narrativized the totality of a previously impenetrable process, allowing that process to be turned over in the mind and perceived in new ways. Evolution (Wright) and epigenesis (Waddington) remained obscure and hotly debated, but in each case were understood to be open to direct investigation through the medium of the model: although these landscapes might seem merely illustrative, in practice they mediated the truth conditions of the theories they represented. For both Wright and Conrad, these landscapes mapped onto concrete biological processes which were possible to investigate empirically. It thus mattered ontologically how one traversed the surface, and where one ended up.¹³

Even before World War Two, then, we find prominent examples of spatial, narrative, and navigational frameworks for understanding abstract mathematical relationships. All share visual conventions familiar from topographic maps and a vocabulary of landscape, ascending, and descending. These stylistic conventions were deployed to explain more intuitively how relationships within systems changed in predictable ways. Researchers imagined symbolic landscapes representing abstract variables, and then placed the elements that they wanted to understand on those landscapes, watching their protagonists move through the world and narrating that movement to say something meaningful about the system as a whole. By the time Curry offered his distillation of Cauchy’s method in 1944, discourses of navigation and landscape were already pervasive across a number of scientific fields.¹⁴

III. The Unknown

The third pathway I trace, joining with the two just described, addresses the importance of digital computation to the method’s broad adoption, as well as some of the epistemological quandaries practitioners began to encounter along the way. The arrival of digital computation greatly extended the gradient method’s utility, allowing it to be applied to problems that would have previously remained utterly unworkable for reasons of time and labor. Gradient optimization is nothing if not repetitive, boiling down to the execution of a small number of simple operations—steps—over and over again. Though dreamt up in the nineteenth century, it did not begin to appear as a practical solution to any but the simplest approximation problems until computers made it feasible to undertake the massive number of calculations that such scenarios required.

In the post-war period, methods of optimization that relied on discursive frameworks of landscape and navigation were beginning to be placed directly into the sphere of industrial production. Exemplary is the work of famed statistician George E. P. Box who, along with his colleague K.B. Wilson at Imperial Chemical Industries (ICI)’s Dyestuff Division, used the steepest ascent method to statistically approximate the ideal combination of pressure, temperature, and other variables in the mass production of chemicals (Box & Wilson, 1951). Their key contribution was to use statistical analysis (and the gradient method) to figure out how best to maximize yield and profit, visualizing the process using topographic conventions similar to those deployed by Wright or Waddington in the context of biology. Cauchy’s method for approximating the orbits of stars thus became an instrumental means for reconfiguring the organic composition of capital, driving the extraction of surplus value with newfound calculative exactitude.

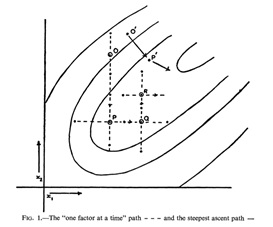
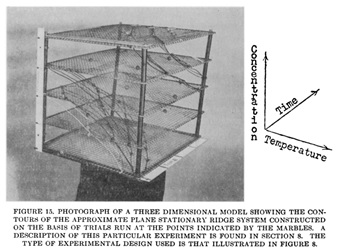
As practitioners began deploying the gradient method in more complex and computationally intensive situations, however, so new kinds of obstacles emerged. Error landscapes do not begin stretched out before us like paintings, available to sight; in this sense, they are radically different than the kinds of landscape that the Romantics so revered. Before they can be graphed, visualized, and described, such surfaces must be explored using an optimization algorithm, revealing the topology of the landscape step by step. For trivial problems, a relatively complete image of the error landscape can be generated, each point corresponding to a different combination of variables, all of which are testable. But as the number of variables and conditions increases, so the number of calculations that would be required to create a complete map increases exponentially as well. In most cases, error surfaces can be grasped and graphed only after the behavior of the function is understood through systemized trial and error search, and this only in the simplest cases. But even if having anything like a total view of the landscape remains unfeasible, the gradient method at least offers a means navigating this unfamiliar terrain: an explorer’s protocol.

In 1951, while Box and Wilson were using topographic language and map-like visualizations to understand and optimize industrial chemical production, they noted in their experiments that sometimes one variable could be changed without affecting yield positively or negatively. This meant that moving in a particular direction on their landscape wouldn’t seem to have any effect whatsoever—they’d effectively found something like a flat spot. The gradient method depends, first, on there being a discernable gradient to follow up or down. What if there isn’t one? Or, worse, what if one climbs up the nearest hill, not realizing that a far higher mountain lies nearby? Lacking a direct, unbroken incline leading to the higher point or more optimized state, and lacking a complete picture of the landscape as a whole, one might easily, Box and Wilson realized, get sidetracked or stuck. What if the place one had arrived, where there was nowhere higher to go, eventually turned out to be an inefficient configuration of variables—a far from optimized state? How would one know, if every incremental step taken from that point would first lead one down? Such anxieties continue to haunt the gradient method wherever it is applied.

This problem—of mistaking a local maxima for the true global maxima—is not an easy one to solve. While computation’s capacity to tackle more laborious optimization scenarios rendered the question of local and global maxima more acute to experimental and applied researchers, the underlying problematic can be observed in any sufficiently complex system when interpreted in terms of gradients. Sewall Wright had already observed a similar problem in evolution: a better (higher) adaptive state might lie across a deep valley from a species’ present location, making it unlikely that the species would evolve in that ‘direction’—doing so would mean first moving down into a less adaptive state. A similar challenge faced Box and Wilson; a researcher, they wrote, ‘will desire to know whether [the surface] probably contains a true maximum (in which case he will wish to estimate its position), a minimax or col (in which case he will wish to know how to ‘climb out of it’), or a ridge (when he will wish to know its direction and slope)’ (Box & Wilson, 1951: 4). Indeed, they lament, ‘in unfortunate cases this summit may be a flat plateau with small curvatures so that the task of obtaining the exact position where the summit occurs may be awkward and exacting, and, in general, is much more difficult’ (Box & Wilson, 1951: 43).

Functions which yield a single global maxima and a smooth gradient that can always be followed towards convergence are known as convex functions, due to the smooth shape of the error surface. Standard gradient optimization will do nicely in these cases if one just keeps climbing. What Box and Wilson describe is a non-convex function with an uncertain and impossible to predict landscape, a mathematical terra incognita. The fundamental problem they identified—the insufficiency of standard gradient optimization in non-convex situations—remains among the most pressing questions in machine learning circles today.

This condition of uncertainty, of not knowing whether one had arrived at a global maxima or merely a local one, was soon internalized within the metaphorical narratives that practitioners were using to intuit and explain their mathematical procedures. In the early 1960s, control theorists Arthur E. Bryson and Walter F. Denham were working on approximating maximum cruising altitudes for aircraft, among other questions in aerodynamics. ‘The problem,’ they said, ‘is to determine, out of all possible programs for the control variables, the one program that maximizes (or minimizes) one terminal quantity’ (1962: 247). Their approach? ‘[E]ssentially a steepest-ascent method and it requires the use of a high-speed digital computer’ (247). Their historic 1962 paper, in addition to deploying gradient optimization, is also credited as one of the first to articulate the method now called backpropagation—though as with so many contributions in the prehistory of machine learning, its originality in this regard was long overlooked.¹⁵

Arthur E. Bryson, the paper’s primary author, was working at Harvard at the time. In the years following World War Two, however, he’d lived in Colorado, where he climbed numerous peaks in the nearby Rocky Mountains. When he decided to leave Cambridge for Stanford in 1968, part of the draw was its setting: “I had in the back of my mind that I loved California […] I liked the west and the Sierras and hiking and climbing” (Bryson, 2016). Though Bryson was born in the lowlands of Indiana, it seems he was a highlander at heart, a climber as well as an engineer and mathematician. Perhaps due to this first-hand experience in the mountains, his paper with Denham describes the challenges posed by the optimization of non-convex functions with striking immediacy:

This process can be likened to climbing a mountain in a dense fog. We cannot see the top but we ought to be able to get there by always climbing in the direction of steepest ascent. If we do this in steps, climbing in one direction until we have traveled a certain horizontal distance, then reassessing the direction of steepest ascent, climbing in that direction, and so on, this is the exact analog of the procedure suggested here in a space of m-dimensions where Φ is altitude and α₁, α₂ are coordinates in the horizontal plane, Fig. 1. There is, of course, a risk here in that we may climb a secondary peak and, in the fog, never become aware of our mistake.

(Bryson & Denham, 1962: 249)

Such is the language of one who has been lost in the mountains before. In this passage, the technical problem of optimization is posed explicitly in terms of judging when one has reached a true summit rather than a false one, and the mathematical condition of uncertainty is incorporated directly into the explanatory narrative as a dense enshrouding fog. Bryson and Denham’s paper, justly celebrated by engineers for its technical achievement, must also be recognized for its descriptive flair: it’s narrative tone and structure metaphorically articulates both the advantages and pitfalls of its method through a mountaineer’s struggle towards the summit.

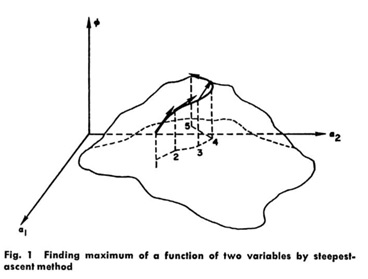
This is the earliest example I have found of a description of the gradient method that incorporates all of what I take to be the core narrative elements in contemporary gradient narratives: a mountainous landscape; a lone protagonist taking methodical steps; a fog (or other narrative device) that obscures the landscape from view and ensures that the way ahead is uncertain; and a predetermined goal that remains easy to articulate (climb to the highest point) but immensely difficult to achieve in practice. Success is never ensured: wemight not reach the top. Each of these narrative elements is now thoroughly conventionalized, as integral to the culture and practice of contemporary machine learning as the methods themselves.

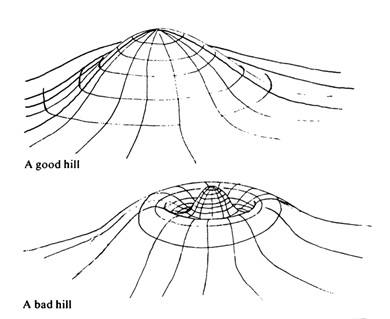
These key elements—a mountain landscape, a lone protagonist taking steps, a fog of uncertainty, and a set goal—are now so standard as to be cliché, repeated again and again in lecture halls, YouTube videos, textbooks, and blog posts, used as readily to explain why a model succeeded as why it failed. Russell and Norvig’s artificial intelligence textbook—a standard reference—simply refers to gradient optimization as ‘hill-climbing search’ (Russell & Norvig, 2010: 122). John D. Kelleher, in his introduction to deep learning, writes that ‘[a]n intuitive way of understanding the process is to imagine a hiker who is caught on the side of a hill when a thick fog descends’ (2019: 196). Other examples, like this one from Pedro Domingos’ book The Master Algorithm, intended for a broad public, are even more fanciful and bizarre:

Imagine you’ve been kidnapped and left blindfolded somewhere in the Himalayas. Your head is throbbing, and your memory is not too good, either. All you know is you need to get to the top of Mount Everest. What do you do? You take a step forward and nearly slide into a ravine. After catching your breath, you decide to be a bit more systematic. You carefully feel around with your foot until you find the highest point you can and step gingerly to that point. Then you do the same again. Little by little, you get higher and higher. After a while, every step you can take is down, and you stop. That’s gradient ascent.

(2015: 110)

Despite its extravagance, for the most part Domingos’ rendition recycles familiar elements from Bryson and Denham’s earlier work. Countless other such examples could be cited, of varying detail and ostentatiousness. Whether framed as an ascent towards the summit or as descent homewards after a long hike, and encompassing numerous variations, the same basic patterns and structure remains. Gradient narratives constitute something of a minor genre all their own, thriving in the interstices of computational knowledge production.

Neural networks are not merely compared based on metrics; like alpinists, they are also judged by how well they navigate a particularly treacherous landscape and celebrated when they arrive at their goal with agility, speed, and grace. In what remains of this essay, I take up the question of mountaineering directly. What does the recurring image of a lone hero lost in the fog on a mountainside tell us about the dreams and desires of contemporary machine learning?

Mount Analog

[W]hat defines the scale of the ultimate symbolic mountain—the one I propose to call Mount Analogue—is its inaccessibility to ordinary human approaches. Now, Sinai, Nebo, and Olympus have long since become what mountaineers call ‘cow pastures’; and even the highest peaks of the Himalayas are no longer considered inaccessible today. All these mountains have therefore lost their analogical importance.

(Daumal, 2019 [1952]: 42-43; emphasis in original)

Gradient narratives about mountain climbing are more than illustrations; they mediate the production and reproduction of today’s computational systems and articulate and reflect something of the ethos of the cultures of which they are a part. Recall that in their computational application of the gradient method to the solving of optimization problems in aerospace engineering, Bryson and Denham wrote that the imagined climbing scenario they described, involving making one’s way uphill step by step while lost in the fog, was an ‘exact analog’ of the technical method itself (Bryson & Denham, 1962: 249). Here, I take Bryson and Denham at their word, and ask: in what ways are mountain climbing and gradient optimization exact analogs of one another?

This is an admittedly strange question, for it seems plain that mathematical optimization could not actually be all that much like mountaineering. Yet the repeated association of the two practices, the constant mapping of optimization as a process upon the mountain landscape, reveals more than the mere conventionalization of a convenient metaphor. Nor do gradient narratives and visualizations of mountain landscapes stand in for processes of optimization only because they are felt to describe the way these systems work in a technically or mathematically precise way. Mountain landscapes also make sense as imagined settings for machine learning to occur for deeper ideological reasons.

In what follows, I address both practices’ shared roots in enlightenment and modernist science, tracing visions of universal man’s capacity to overcome all limits couched in an ethos of progressive self-overcoming. I take the question posed by this analogy to be one that hinges upon a combination of material and historical alignments and ideological and epistemological orientations which are felt to be held in common, whatever the obvious and real dissimilarities which exist between gradient optimization and mountaineering as each is practiced today.

At stake is something like a common ethos, oriented towards a similar dream. Central to both practices, core to both the dream of AGI and the dream of Everest, are two closely related axioms. First, the belief that learning is about directly confronting the unknown, striking out into the world and forging an exploratory path towards growth and knowledge. Cultures of AI and cultures of mountaineering both engage in a productive and constiuitive confrontation with uncertainty: as we have already seen in the case of the gradient method, learning how to address uncertainty constitutes the very core of what it means to optimize, improve, and succeed. Second, there is a certain congruence in method, a common emphasis on a systematic, rigorous, even machinic pushing of perceived limits: a promethean drive to challenge conditions as they are.¹⁷ The mountaineer, striving to tame or even dominate doubt, is thought to approach this quest through a methodical regimen of repetition, training, and the intensification of one’s own resolve. Machine learning’s focus on endless algorithmic repetition and training as a viable path to optimization, learning, and intelligence strikes a similar key.

The tradition of seeking knowledge or transcendence through a direct confrontation with the unknown has deep roots in Western thought. The dream of modern mountaineering, like the dream of AI, inherits much from this tradition, which also celebrates the figure of the lone intrepid seeker as the propeller of progress. Mary Terrall has noted the importance of images and practices of exploration and travel in the constitution of Enlightenment ideals: since the age of Descartes, ‘[p]hysical exertion and exploration came to be associated with discovery and understanding, and played an important part in establishing scientific reputations’ (1998: 224). Terrall also notes that in this context, the metaphor of ‘clear sight’ was joined with that of ‘moving through uncharted territory’, establishing an ethos which emphasized the direct confronting of obscurity and illusion by literally and figuratively taking to the hills (1998: 224). Thus, when John Hunt, the leader of the successful Everest expedition which put Edmund Hillary and Tenzing Norgay on the summit, wrote of ‘the possibility of entering the unknown’, he was already on well-trod ground (1954: 8).¹⁸

Such values, of course, were inherently gendered and raced, establishing the white male subject as the privileged protagonist of knowledge and of history.¹⁹ Though challenged from within and without, such values continue to inflect the cultures of both mountaineering and AI.²⁰ Like digital computation, mountaineering saw a very public renaissance in the years following World War Two. Overdeveloped nations, seeking redemption from the ravages of war, funded expeditions around the world—frequently with neocolonial undertones. As Peter H. Hansen has argued, in the post-war era the perennial obsession with ‘who was first’ on a summit reflected a particular matrix of concerns bound up with modern understandings of civilizational progress, the demystification of nature, and the sovereignty of individual man, all articulated against the geopolitical backdrop of the Cold War (2013: 272). With the reconfiguration of global power, competition for the conquest of high unclimbed peaks became a key arena of geopolitical struggle, as well as a global stage where men, often white, straight, and from the Global North, competed to win recognition and fame. Many post-war expeditions were led by former officers who had served in their countries’ war efforts; they brought their discipline, training, and militaristic sensibilities along with them. They spoke of laying siege to the Himalaya, winning glory for their countries and renown for themselves.

Mountains were far more than geopolitical proxies, however. Insofar as they symbolized a confrontation with and challenge to the unknown, they were also terrains upon which ideas about the capacities and limits of the human were forged. Mountaineering as a cultural practice was (and remains) not merely a secondary effect or consequence of its milieu; the practice itself has helped constitute and delineate modern notions of individual subjectivity and masculinity. Whatever national priorities it inevitably reflected in the post-war era, the mountain landscape also increasingly became the preeminent site for demonstrations of individual willpower, settings where the contours of the heroic subject were tested and defined. These were places where individuals went to challenge the unknown with the goal of overcoming it; places of colonial and masculinist confrontations with nature and the self. Places, in other words, to put a great modern question to the test: what is the human capable of?

We can hear echoes of such a question refracted through the posthuman drive to build machines which can best the human on its home turf. When it is recognized that the same historical era which saw the birth of modern AI research in the 1950s also witnessed the scaling of many of the world’s highest peaks, the projection of heroic mountaineering narratives onto the quest for transcendent artificial intelligence begins to make perfect sense. Mountain climbing, particularly at mid-century, was an intensely promethean undertaking; the whole mountaineering mise-en-scène, reverberating with powerful cultural associations of progress, of rising to challenges and overcoming them, speaks to something of the macho bravura with which AI boosters proclaim the inevitable singularity. Though contemporary mountaineering culture has mercifully begun to temper its more jocular ambitions, the myth of the climber as autonomous hero remains as pervasive as ever. Realizing human-level AI is felt to represent a daring conquest of the impossible, just as the scaling the world’s highest mountains once did. And if, indeed, the realization of human potential on the summit of a peak can be boiled down to the practice of navigating a mountainous landscape step by step, then the possibility of achieving artificial general intelligence through a doubling down on incremental gradient methods and brute force computation appears palpably within reach.

I am arguing here that whatever pragmatic explanatory power these gradient narratives undeniably hold for machine learning practitioners, the appropriation of the imagery and language of mountains and mountaineering also echoes with a particular mode of engagement with the world all too familiar to mountaineering mythologies: one that Nicola Masciandaro has characterized as ‘an overcoming-by-intensifying of its own problematic’ (2018: 90). At stake is a systematic and rigorous challenging of perceived limits, but articulated through an intensification and concentration of one’s core potentialities: the very essence of optimization itself. Marget Grebowicz has argued that ‘[t]oday’s climbing body is more often than not presented as a convergence of the values of performance, speed, and efficiency, in perfect compliance with neoliberal fantasies of the individual who overcomes adversity as well as with biopower’s demand for docile bodies’ (2018: 94). With this in mind, it should hardly be surprising that an ideological figure representing the optimized, autonomous subject—the mythic self-overcoming mountaineer—has been widely appropriated to represent and anthropomorphize a machine that, some imagine, will one day surpass the human entirely.

Narrative, as N. Katherine Hayles has insisted, ‘is essential to the human lifeworld’ (2007, 1606). The narratives I have described constitute the frames through which an ethos of optimization in the face of uncertainty is articulated today. No less than the calculations they allegorize, gradient narratives are core to the theorization and enactment of machine learning as a sociocultural practice; as explanatory myths, gradient narratives are constitutive of the gradient method’s cultural solidity and productive value. As interpretive frames, mountain landscapes mediate discourses and understandings of what ‘optimization’ and ‘learning’ mean; they color what neural networks are imagined to be capable of doing and reflect how practitioners conceive and design them in the first place. Gradient narratives are simultaneously pragmatic heuristic concepts for the production of machine learning systems in metric societies and expressions of an ideology, a whole way of orienting the self to the world.

The mountain landscape has long been seen as the crucible and natural scene for the self-improvement of the autonomous subject through training, exertion, and confronting the unknown, and as long as there are mountains this is likely to remain true for many. I have argued that the legacy of particular cultural associations is one reason why the mountain landscape lends itself so easily as a backdrop to a project which explicitly seeks to overturn inherited notions of what is possible. Mountains have long been thought of as proving grounds for humans; why not, it seems, for machines?

While gradient narratives today draw upon older cultural and linguistic formations allegorizing and internalizing certain masculinist approaches to mountaineering, this is not to say that less individualist and domineering modes of climbing, and perhaps too of something like machinic optimization, are possible. After all, there are many ways to encounter mountains; there are also many ways to confront and imagine the nonhuman capacities of a machine. We need not necesarrily discard our inherited metaphors wholesale, but further attention to their histories and undertones might allow us to ask better questions of the mandate to ascend and to master the landscape at any cost.²²

Acknowledgements

This essay benefitted greatly from the collective labor and attention of many friends, colleagues, and mentors, without whose help the climb to the summit would have been insurmountable. In the spirit of collective knowledge, I recognize and thank them for their assistance and care.

The Digital Theory Lab at NYU has provided a stimulating academic arena for critical engagement with computation and artificial intelligence over the past few years, and this essay is a direct outcome of our many conversations and debates; I thank all my fellow participants, and in particular Leif Weatherby and Joseph Lemelin for coordinating such a generative space. In the Department of Media, Culture, and Communication at NYU, Alexander Galloway and Erica Robles-Anderson provided critical feedback on early drafts, and Nicole Starosielski and Finn Brunton each posed insightful questions and suggestions. I thank the editors at Culture Machine for their thorough attention, and the two anonymous reviewers whose thoughtful and constructive comments contributed to a substantial rethinking of this essay. I am grateful for numerous informal conversations with machine learning practitioners in New York and beyond, and to the researchers who so graciously allowed me to reproduce their compelling visualizations in this essay. Finally, I extend my utmost gratitude to my writing collective—Karly Alderfer, Alexander Campolo, Jeanne Etelain, Alexander Miller, Pierre Schwarzer, and Yuanjun Song—comrades, all, in the pursuit of critical thought and clear prose.

Author Bio

Sam P. Kellogg is a writer, researcher, editor, teacher, and trekking guide. He is a PhD candidate in the department of Media, Culture, and Communication at New York University. When not on a mountain, he lives in Rockaway Beach, New York City.

Website: samkellogg.com

Notes

1. There is a lineage to such accusations; the Heideggerian philosopher Hubert Dreyfus famously charged another branch of AI research (one not reliant on gradient optimization) with alchemy in the 1960s (Dreyfus, 1965).

2. N. Katherine Hayles has argued that we include such processes under the heading of ‘non-conscious cognition’ (Hayles, 2017). We might then understand gradient narratives as technosocial myths that aim at understanding the behavior of non-conscious cognizers in more familiar humanistic terms.

3. My approach draws inspiration from Anna Tsing’s work on anthropogenic landscapes in Denmark—very different sorts of landscape than those dealt with here. Tsing grapples with the question of how to keep many different timescales and timelines in view at once, without imposing something like a master frame. ‘Consider,’ Tsing suggests, ‘the key dates currently in play for the beginning of the Anthropocene. These dates are competing entries—but here I make them points for noticing landscape change’ (2017: 8). Rather than assert the absolute primacy of one date in particular, Tsing instead takes each one into account in as offering a different ‘high’ point ‘from which to watch for something new’ (2017: 8).

4. See, for example, Chris Anderson’s mosquito-based explanation (2019).

5. Narratives set in imaginary mathematical spaces are hardly new. Edwin A. Abbott’s Victorian fantasy novel Flatland: A Romance of Many Dimensions, first published in 1884, is perhaps the most widely known example (Abbott, 2002).

6. Drawing on Alexander R. Galloway’s understanding of the digital and the analog, the gradient method could be productively considered a digital method for dealing with analog phenomena. It is digital because it proceeds by individuated, discrete steps, and because of its association with walking and the foot (digits: fingers and toes)—characteristics aligned with digitality. Yet the method also requires and even presupposes a continuous underlying phenomenon, a curve or smooth transition, in order to make any progress—features associated with a condition of analogicity. The fact that these two modes comingle and thrive together within contemporary machine learning, even if the analog appears in simulated form, lends credence to the hypothesis that the distinction between the analog and the digital is rarely absolute in practice; one can deal with analogicity using digital means and vice versa. We could productively consider the gradient method as essentially a form of sampling: a digital technology for handling a continuous phenomenon and moving, step-wise, along it. (Galloway, 2014: xxviii-xxix; 2020).

7. Peter Debye, for example, described a version of the gradient method in a paper in 1909, drawing upon unpublished work by Bernhard Riemann from 1863. Both were oblivious of Cauchy’s formulation (Petrova & Solov’ev, 1997).

8. Haskell, a student of David Hilbert, also worked on the ENIAC project after the war, and his work is foundational in many branches of computer science. There are no fewer than three programming languages named after him.

9. Curry notes that, even when it was used, it was frequently misattributed; Curry cites Cauchy as the method’s progenitor (Curry, 1944: 258-259).

10. The context of this quote is a brief comparison with a similar method outlined by Kenneth Levenberg, also at the Frankford Arsenal’s Fire Control Design Division (Levenberg, 1944). Interestingly, Curry differentiates his method from Levenberg’s by noting that Levenberg’s approach, to its detriment, follows a “broken path” (Curry, 1944).

11. I struggled over how best to describe gradient optimization and whether or not to fall back on the topographical language which this paper addresses, but the only alternative seemed to be merely presenting the algorithm as an equation. I take this difficulty as evidence for how constitutive such language and imagery is to the method’s use and longevity in the field. As Juliette Kennedy has argued, ‘the mathematician,’ (and, we might add, the computer scientist or machine learning practitioner), ‘grounds herself in natural language – and in the production of images’ (2017: 72; emphasis original).

12. Of relevance to machine learning, Gibbs is also credited as one of the founders of modern vector analysis (Crowe 1985).

13. Let me emphasize that these two landscapes represent fundamentally different processes, in different strands of biology, with different priorities and histories; despite a certain resemblance (and indeed Wright reportedly inspired Waddington), they should not be confused. Here, I am most interested in exploring the formal similarities of the two models, which bear so much resemblance to those of contemporary machine learning. Readers curious about Wright’s model and its legacy should begin by consulting Svensson and Calsbeek’s excellent 2013 volume, as well as Skipper (2004), Johnson (2008), Petkov (2015), and Pigliucci (2008). For Waddington’s landscape, consult Jan Badke’s insightful 2013 paper and Susan Merrill Squier’s generative 2017 book, as well as Haraway (2004: 59-61).

14. Yet another example is found in physical chemistry, with the influential concept of the resonance energy surface developed by Henry Eyring and Michael Polanyi in 1931. This surface was also graphed using the familiar altitudinal lines from topographic cartography (Eyring & Polanyi, 2013 [1931]; Nye, 2007).

15. Rumelhart et al.’s seminal 1986 paper is credited with drawing attention to backpropagation as a method to AI researchers. But as has been broadly recognized at least since Dreyfus’ 1990 paper, Bryson and Denham’s contribution, alongside a 1960 paper by Henry J. Kelley on optimal flight pathing, articulated essentially the same approach to optimization decades beforehand. Considering what a breakthrough backpropagation proved to be once it was adopted by AI researchers, one wonders what other underused methods lie dormant in unrelated fields today (Dreyfus, 1990; Goodfellow et al., 2016; Kelley, 1960; Rumelhart et al., 1986; Schmidhuber, 2015).

16. In his work on Jacques Bertin and data visualization, Alexander Campolo has drawn attention to structuralist efforts to render excesses of abstract quantitative data more immediately graspable and intuitive; for the graphical theorists he studies, ‘[v]isualization conditions how data can be made intelligible and comparative, how they can be rendered empirical’ (2020: 47). Such an impulse to render data ‘empirical’ through visualization, thereby demystifying obscure algorithmic processes, is common in contemporary machine learning discourse.

17. Not for nothing was Ueli Steck, perhaps the most celebrated alpinist of his generation who passed away in a climbing accident in 2017, known by the nom de guerre the ‘Swiss Machine’.

18. I credit Margret Grebowicz’s critical work on climbing for drawing my attention to this luminous line by Hunt (Grebowicz, 2018: 91).

19. On the whiteness of AI, see Cave and Dihal (2020).

20. Adequately addressing these question remains beyond the scope of this paper, suffice to say I take most of these ‘failures’ to be reflective of larger structural inequalities and patterns of violence rather than easily isolated technical hiccups. As such they are not amenable to solving with optimization algorithms. Such is the case of racist housing, employment, and sentencing algorithms in the United States, for example, where, as Christina Sharpe argues, white supremacy and anti-Blackness constitute part of a ‘total climate’ which would necessarily be reflected in the contours of the surfaces that algorithms traverse (Sharpe, 2016).

21. National teams from around the world were fiercely competing for first ascents in those years; Edmund Hillary and Tenzing Norgay’s ascent of Everest in 1953 would be claimed by Great Britain, New Zealand, India, and Nepal as national triumphs of the first order (Hansen, 2013: 245). 22. Amrita Dhar, among others, is pursuing vital research rewriting dominant histories of mountaineering and surfacing overlooked contributions from racialized and colonized others. In so doing, she is also challenging the image of the lone man victorious on the summit—an old and persistent myth—thereby changing understandings of what summiting a mountain truly costs, and who, beyond the summit team, is responsible for such an achievement (2016).

---

References

Abbott, E. A. (2002) The Annotated Flatland: A Romance of Many Dimensions. Edited by I. Stewart. New York, NY: Basic Books.

Agre, P. E. (1997) ‘Toward a Critical Technical Practice: Lessons Learned in Trying to Reform AI’, in Bowker, G. C. et al. (eds) Social Science, Technical Systems and Cooperative Work: Beyond the Great Divide. Mahwah, NJ: Lawrence Erlbaum Associates.

Amini, A. et al. (2019) ‘Spatial Uncertainty Sampling for End-to-End Control’, arXiv:1805.04829.

Anderson, C. (2019) ‘Gradient Decent’, in Brockman, J. (ed.) Possible Minds: 25 Ways of Looking at AI. New York, NY: Penguin.

Appadurai, A. & Kift, P. (2020) ‘Beware the magic of metrics’, Eurozine. https://www.eurozine.com/beware-the-magic-of-metrics/ (Accessed: 20 July 2020).

Bachelard, G. (1964) The Poetics of Space. Trans. M. Jolas. New York, NY: Penguin.

Baedke, J. (2013) ‘The epigenetic landscape in the course of time: Conrad Hal Waddington’s methodological impact on the life sciences’, Studies in History and Philosophy of Biological and Biomedical Sciences 44 (4B): 756–773.

Box, G. E. P. (1954) ‘The Exploration and Exploitation of Response Surfaces: Some General Considerations and Examples’, Biometrics 10 (1): 16–60.

Box, G. E. P. & Wilson, K. B. (1951) ‘On the Experimental Attainment of Optimum Conditions’, Journal of the Royal Statistical Society. Series B (Methodological) 13 (1): 1–45.

Bryson, A. E. (2016) ‘Oral History’. https://purl.stanford.edu/vz888mz5394 (Accessed: 18 August 2020).

Bryson, A. E. & Denham, W. F. (1962) ‘A Steepest-Ascent Method for Solving Optimum Programming Problems’, Journal of Applied Mechanics 29 (2): 247–257.

Callon, M. (1984) ‘Some elements of a sociology of translation: domestication of the scallops and the fishermen of St Brieuc Bay’, The Sociological Review 32: 196–233.

Campolo, A. (2020) ‘Signs and Sight: Jacques Bertin and the Visual Language of Structuralism’, Grey Room 78: 34–65.

Cauchy, A. (1847) ‘Méthode générale pour la résolution des systèmes d’équations simultanées’, in Académie des sciences, Comptes rendus hebdomadaires des séances de l’Académie des sciences. Paris: Gauthier-Villars.

Cave, S. and Dihal, K. (2020) ‘The Whiteness of AI’, Philosophy & Technology 33: 685–703.

Crowe, M. J. (1985) A History of Vector Analysis: The Evolution of the Idea of a Vectorial System. New York, NY: Dover.

Curry, H. B. (1944) ‘The method of steepest descent for non-linear minimization problems’, Quarterly of Applied Mathematics 2 (3): 258–261.

Dhar, A. (2016) ‘The Matter of History: Himalayan Mountaineering, its Archives & some Inexcusable Gaps’, Humanities Underground. Available at: http://humanitiesunderground.org/the-matter-of-history-himalayan-mountaineering-its-archives-some-inexcusable-gaps/ (Accessed: 30 July 2020).

Domingos, P. (2015) The Master Algorithm: How the Quest for the Ultimate Learning Machine Will Remake Our World. New York, NY: Basic Books.

Dragicevic, P., Jansen, Y. & Vande Moere, A. (2020) ‘Data Physicalization’, in Vanderdonckt, J. (ed.) Springer Handbook of Human Computer Interaction. Springer Reference.

Dreyfus, H. L. (1965) Alchemy and Artificial Intelligence. Rand Corporation. Available at: https://www.rand.org/pubs/papers/P3244.html.

Dreyfus, S. E. (1990) ‘Artificial neural networks, back propagation, and the Kelley-Bryson gradient procedure’, Journal of Guidance, Control, and Dynamics 13 (5): 926–928.

Eyring, H. & Polanyi, M. (2013) ‘On Simple Gas Reactions’, Zeitschrift für Physikalische Chemie 227 (11): 1221–1246.

Galloway, A. R. (2014) Laruelle: Against the Digital. Minneapolis, MN: University of Minnesota Press.

Galloway, A. R. (2020) ‘Transcoding, Transduction, Sampling, and Interpolation — The Four Interfaces’, Alexander R. Galloway. Available at: http://cultureandcommunication.org/galloway/transcoding-transduction-sampling-and-interpolation-the-four-interfaces (Accessed: 20 December 2020).

Goodfellow, I. J., Bengio, Y. & Courville, A. (2016) Deep Learning. Cambridge, MA: The MIT Press.

Grebowicz, M. (2018) ‘The Problem of Everest: Upward Mobility and the Time of Climbing’, the minnesota review 90: 91–99.

Hansen, P. H. (2013) The Summits of Modern Man: Mountaineering After the Enlightenment. Cambridge, MA: Harvard University Press.

Haraway, D. J. (2004) Crystals, Fabrics, and Fields: Metaphors that Shape Embryos. Berkeley, CA: North Atlantic Books.

Hayles, N. K. (2007) ‘Narrative and Database: Natural Symbionts’, PMLA 122 (5): 1603–1608.

Hayles, N. K. (2017) Unthought: The Power of the Cognitive Nonconscious. Chicago, IL: The University of Chicago Press.

Herzog, M. (1952) Annapurna: First Conquest of an 8000-meter Peak [26,493 feet]. Translated by N. Morin and J. A. Smith. New York, NY: E. P. Dutton & Company.

Hohl, L. (2012) Ascent. Trans. D. Stonecipher. New York, NY: Black Square Editions.

Hunt, J. (1954) The Conquest of Everest. New York, NY: Dutton.

Hutson, M. (2018) AI researchers allege that machine learning is alchemy, Science. Available at: https://www.sciencemag.org/news/2018/05/ai-researchers-allege-machine-learning-alchemy (Accessed: 14 August 2020).

Jameson, F. (1972) The Prison-House of Language: A Critical Account of Structuralism and Russian Formalism. Princeton, NJ: Princeton University Press.

Jameson, F. (1992) The Geopolitical Aesthetic: Cinema and Space in the World System. Bloomington, IN: Indiana University Press.

Johnson, N. (2008) ‘Sewall Wright and the Development of Shifting Balance Theory’, Nature Education 1 (1).

Kelleher, J. D. (2019) Deep Learning. Cambridge, MA: The MIT Press.

Kelley, H. J. (1960) ‘Gradient Theory of Optimal Flight Paths’, ARS Journal 30 (10): 947–954.

Kennedy, J. (2017) ‘Notes on the Syntax and Semantics Distinction, or Three Moments in the Life of the Mathematical Drawing’, in Coles, A., de Freitas, E., and Sinclair, N. (eds) What is a Mathematical Concept? Cambridge, UK: Cambridge University Press: 55–75.

Lakoff, G. & Johnson, M. (1980) Metaphors We Live By. Chicago, IL: The University of Chicago Press.

Lemarechal, C. (2012) ‘Cauchy and the Gradient Method’, Documenta Mathematica Extra Volume: Optimization Stories: 251–254.

Levenberg, K. (1944) ‘A Method for the Solution of Certain Non-Linear Problems in Least Squares’, Quarterly of Applied Mathematics 2 (2): 164–168.

Li, H. et al. (2018) ‘Visualizing the Loss Landscape of Neural Nets’, arXiv:1712.09913.

Masciandaro, N. (2018) ‘Introduction’, the minnesota review 90: 89–90.

Maxwell, J. C. (1875) Theory Of Heat. Fourth Edition. London, UK: Longmans, Green, and Company.

Minsky, M. and Papert, S. A. (1987) Perceptrons: An Introduction to Computational Geometry. Expanded Edition. Cambridge, MA: The MIT Press.

National Museums Scotland (n.d.) James Clerk Maxwell’s thermodynamic surface, National Museums Scotland. https://www.nms.ac.uk/explore-our-collections/stories/science-and-technology/james-clerk-maxwell-inventions/james-clerk-maxwell/thermodynamic-surface (Accessed: 18 August 2020).

Nye, M. J. (2007) ‘Working Tools for Theoretical Chemistry: Polanyi, Eyring, and Debates Over the “Semiempirical Method”’, Journal of Computational Chemistry 28 (1): 98–108.

Oxford English Dictionary (2020) ‘grade, n.’, Oxford English Dictionary Online. Oxford, UK: Oxford University Press.

Parisi, L. (2019) ‘Critical Computation: Digital Automata and General Artificial Thinking’, Theory, Culture & Society 36 (2): 89–121.

Parker-Holder, J. et al. (2020) ‘Ridge Rider: Finding Diverse Solutions by Following Eigenvectors of the Hessian’, arXiv:2011.06505.

Petkov, S. (2015) ‘The Fitness Landscape Metaphor: Dead but Not Gone’, Philosophia Scientiæ. Travaux d’histoire et de philosophie des sciences 19 (1): 159–174.

Petrova, S. S. & Solov’ev, A. D. (1997) ‘The Origin of the Method of Steepest Descent’, Historia Mathematica 24 (4): 361–375.

Pigliucci, M. (2008) ‘Sewall Wright’s adaptive landscapes: 1932 vs. 1988’, Biology & Philosophy 23 (5): 591–603.

Rosselli, C. (1481) Descent from Mount Sinai (Sistine Chapel). Available at: https://en.wikipedia.org/wiki/Descent_from_Mount_Sinai_(Sistine_Chapel).

Ruder, S. (2017) ‘An overview of gradient descent optimization algorithms’, arXiv:1609.04747.

Rumelhart, D. E., Hinton, G. E. & Williams, R. J. (1986) ‘Learning representations by back-propagating errors’, Nature 323 (9): 533–536.

Russell, S. J. & Norvig, P. (2010) Artificial Intelligence: A Modern Approach. 3rd edn. Upper Saddle River, NJ: Prentice Hall.

Schmidhuber, J. (2015) ‘Deep learning in neural networks: An overview’, Neural Networks 61: 85–117.

Sharpe, C. (2016) In the Wake: On Blackness and Being. Durham, NC: Duke University Press.

Skipper, Jr., Robert A. (2004) ‘The Heuristic Role of Sewall Wright’s 1932 Adaptive Landscape Diagram’, Philosophy of Science, 71(5): 1176–1188.

Squier, S. M. (2017) Epigenetic Landscapes: Drawings as Metaphor. Durham, NC: Duke University Press.

Svensson, E. & Calsbeek, R. (eds) (2013) The Adaptive Landscape in Evolutionary Biology. Oxford, UK: Oxford University Press.

Terrall, M. (1998) ‘Heroic Narratives of Quest and Discovery’, Configurations 6 (2): 223–242.

Tsing, A. L. (2017) ‘The Buck, the Bull, and the Dream of the Stag: Some unexpected weeds of the Anthropocene’, Suomen Antropologi: Journal of the Finnish Anthropological Society, 42 (1): 3–21.

Waddington, C. H. (1957) The Strategy of the Genes: A Discussion of Some Aspects of Theoretical Biology. London, UK: Routledge.

Wilson, E. B. (1936) ‘Papers I and II as Illustrated by Gibbs’ Lectures on Thermodynamics’, in Donnan, F. G. and Haas, A. E. (eds) A commentary on the scientific writings of J. Willard Gibbs, Volume 1: Thermodynamics. New Haven, CT: Yale University Press.

West, T. G. (1999) ‘Images and reversals: James Clerk Maxwell, working in wet clay’, ACM SIGGRAPH Computer Graphics 33 (1): 15–17.

Wright, S. (1932) ‘The roles of mutation, inbreeding, crossbreeding and selection in evolution’, in Jones, D. F. (ed.) Proceedings of the 6th International Congress in Genetics. Ithaca, NY: International Congress of Genetics.